Дельфис

Одна из важнейших характеристик развития современной цивилизации — рост народонаселения. Закономерности роста обычно изучаются без учёта реинкарнации. Считается, что живой организм (в том числе человек) рождается от родительских организмов (родительской пары), которая передаёт ему «управляющую систему», позволяющую строить из косной материи клетки и ткани нового организма. Генетическая структура организма, полученная в наследство от зародышевых клеток, контролирует процессы обмена в народившемся организме. Когда организм погибает (в результате болезни, несчастного случая, насилия или от старости), его жизнь полностью прекращается, а организованная материя, составлявшая организм, возвращается в исходное неорганизованное состояние. Такова в общих чертах точка зрения нашей западной науки. Наряду с ней существует весьма развитая культурная традиция, имеющая очень древние корни, в которой процессы рождения и смерти трактуются как процессы обмена, взаимодействия двух миров — тонкого и физического. Согласно этой традиции, изучаемые современной наукой закономерности рождения, роста и старения организма относятся только к физическому телу. Прирост населения, представляющий собою баланс между рождаемостью и смертностью, определяется движением (циркуляцией) населения по двум мирам — тонкому и физическому (плотному). Следовательно, необходимо учитывать взаимодействие этих миров. Мы попытаемся рассмотреть процесс воспроизводства и роста населения в плотном мире как часть общего процесса циркуляции населения по обоим мирам.

Обратимся вначале к эмпирическим данным, относящимся к физическому миру.

1. Эмпирический закон роста народонаселения

Прирост народонаселения определяется разностью между рождаемостью и смертностью, и за единицу времени он равен:

∆N = n-m,       (1)

где n и m, соответственно, рождаемость и смертность в единицу времени.

Статистические данные показывают, что абсолютный прирост населения ∆N пропорционален численности населения N. Значит, прирост dN за малое время dt составляет величину:

dN = qN(t)dt,      (2)

где q — коэффициент пропорциональности. При dt=1 имеет место: q = dN/N, то есть q является относительным приростом населения в единицу времени. В статистических данных обычно приводится прирост на тысячу человек в год. Если относительный прирост неизменен (q=q_o=const), то, согласно уравнению (2), изменение численности происходит по экспоненциальному закону:

N = N_o exp(q_ot) = N_oe^q_o^t      (3)

где N_o — численность населения в момент времени t = о.

Относительный прирост q зависит от ряда факторов — биологических, географических, исторических, экономических, психологических, социокультурных. Поскольку эти факторы, во всяком случае некоторые из них, меняются с течением времени, относительный прирост q, вообще говоря, есть функция времени (q = q(t)), и закон роста народонаселения отличается от экспоненциального.

Как реально растёт народонаселение на Земле? Что говорят статистические данные? Согласно оценкам специалистов [1], с.31 , в очень давние времена — от 1000000 до 6000 лет до н.э. — численность населения практически не менялась со временем, составляя 2÷5 млн. человек. Начиная примерно с 6000 г. до н.э., отмечается рост народонаселения. В период с 6000 по 3000 гг. до н.э. численность населения составляла 5÷20 млн. чел., с 3000 по 2000 гг. до н.э. — 20÷40 млн. чел., с 1000 г. до н.э. по 250 г. н.э. — 100÷200 млн. чел. и с 250 по 1500 гг. — 300÷400 млн. человек. Конечно, эти оценки весьма приблизительные. Согласно справочнику Урланиса [2], с.8, население мира составляло:

Население

Более поздние данные можно найти в Статистических Ежегодниках ООН [3].

На рисунке 1 показано, как менялась численность населения Земли за период от 6000 г. до н.э. по настоящее время. По горизонтальной оси отложено время t, по вертикальной — численность населения в логарифмическом масштабе (log N). Если бы население росло строго экспоненциально, то на этом графике мы должны были бы получить прямую линию. В действительности, линия, выражающая рост народонаселения со временем, начиная приблизительно с середины 2-го тысячелетия, заметно отклоняется от прямой, причём уходит вверх всё круче и круче. Более детально это видно на рисунке 2. Значит, относительный годовой прирост постоянно возрастает. В этом и состоит особенность современной демографической ситуации: не только увеличивается абсолютная численность населения N, но и возрастают среднегодовые темпы роста, то есть относительный прирост населения q. Как быстро увеличивается прирост населения?

^{Рис.1. Численность населения на земном шаре, согласно оценкам [1] - [2]. По вертикальной оси - численность населения в логарифмическом масштабе}

^{Рис.2. Рост численности населения на Земле [2] - [3]. По вертикальной оси — численность населения в логарифмическом масштабе}

^{Рис.3. Гиперболический закон роста народонаселения по И.С.Шкловскому [5]. По вертикальной оси — обратная величина численности населения}

2. «День Страшного суда»

В 1960 году в журнале «Science» была опубликована статья трёх авторов — Х.Форстера, П.Мора и Л.Эмиота под названием «День Страшного суда: четверг, 13 ноября 2026 года новой эры» [4]. Используя тщательно отобранные статистические данные, авторы показали, что относительный прирост населения увеличивается так же быстро, как само население, то есть

q(t) = q_oN(t).      (4)

Подставляя это выражение в (2), найдём:

dN = q_o[N(t)]²dt.      (5)

Чем объясняется подобная зависимость, остаётся неясным. Выражению (5) отвечает следующий закон роста народонаселения¹:

N(t) = 1/q_o(t_*-t).      (6)

Нетрудно узнать в выражении (6) уравнение гиперболы. Следовательно, численность народонаселения изменяется по гиперболическому закону. При некотором времени t = t_*, население Земли должно достичь бесконечности (N(t) = ∞ )! Когда наступит этот роковой момент? Неожиданный результат расчётов заключается в том, что он совсем «не за горами». Согласно вычислениям авторов, такое должно произойти в 2026 году, точнее, при t_* = 2026,87+5,5, если время t отсчитывается от начала новой эры.

Если величина t_* определена, можно, откладывая по оси абсцисс значения log(t_* - t), а по оси ординат значения log N, построить график зависимости (6) в виде прямой линии с отрицательным наклоном, равным -1. При условии t → t_*-и прямая ЛИНИЯ устремляется в бесконечность. Момент и на графике определить невозможно, ибо при t = t_* логарифм становится бесконечным (log(t_* - t) = - ∞). В своё время профессор И.С.Шкловский нашёл убедительный способ наглядно продемонстрировать справедливость гиперболического закона, не зная величины t_* [5]. Обозначим величину 1/N через у, тогда выражение (6) примет вид:

y = q_o(t_*-t).      (7)

А это есть уравнение прямой. Следовательно, при построении графика, на котором по горизонтальной оси отложено время t, а по вертикальной — величина у = .1/N, мы должны получить прямую линию. Рисунок 3 иллюстрирует сказанное. Причём статистические данные (точки на графике) почти без всякого отклонения ложатся на эту прямую. При t = t_* имеем у = о, и следовательно, прямая пересекает ось абсцисс в точке, соответствующей t = t_*. Таким образом можно грубо оценить этот особый момент непосредственно по графику — как точку пересечения прямой линии с осью абсцисс, а более точно его можно вычислить, например, методом наименьших квадратов. Для прямой, изображённой на рисунке 3, критический момент t_* соответствует 2028 году.

3. Смена закона

Итак, в настоящее время население Земли растёт по гиперболическому закону. Но каковы границы его применимости? Экстраполяция гиперболического закона в прошлое показывает, что он удовлетворительно согласуется с оценками численности населения на интервале времени порядка одного миллиона лет [6]. Однако дальнейшая экстраполяция в прошлое приводит к неправдоподобным и даже абсурдным результатам: так, согласно гиперболическому закону, в момент возникновения физической Вселенной (около 20 млрд. лет тому назад) на Земле уже жило 10 человек; а время возникновения первого человека (N = 1) уходит в прошлое на 200 млрд. лет, то есть задолго до возникновения Земли, Солнечной системы и всей Метагалактики.

Согласно исследованиям С.П.Капицы, в эпоху, предшествующую палеолиту, население Земли росло пропорционально ctg(-t), и около 1,6 млн. лет тому назад этот закон сменился на гиперболический. Если бы гиперболический закон был справедлив вплоть до рокового момента t_*, это бы означало, что численность населения за конечный промежуток времени увеличивается до бесконечности. Очевидно, это невозможно, ибо требует бесконечно быстрого прироста населения, а он ограничен естественными биологическими причинами (фертильность — способность организма производить потомство — не может быть бесконечной!), не говоря уже об экономических и социокультурных факторах. Отсюда следует, что гиперболический закон нельзя экстраполировать до значений, сколь угодно близких к моменту времени t». При некотором меньшем значении (t < t_*) гиперболический закон роста теряет силу и должен смениться новым демографическим законом. А так как значение t_* близко к современному моменту, то смена демографического закона должна произойти в самое ближайшее время (а возможно, уже происходит).

На рисунке 3 прямая линия построена по данным о численности народонаселения до 1970 года (эти данные изображены на рисунке кружками, тёмные точки — более поздние данные, относящиеся к 1987 и 1991 годам). Как видно, вплоть до начала до-90-х годов гиперболический закон всё ещё сохранял силу. Это связано с влиянием развивающегося мира. Для развитых стран прирост населения прошёл через максимум и начал замедляться в середине XX века. Но динамика роста населения Земли определяется развивающимися странами, а здесь прирост населения до последнего времени, видимо, продолжал увеличиваться. Тем не менее, ясно, что в ближайшее время ситуация должна измениться, и отклонения от гиперболического закона для всего населения Земли станут ощутимы.

Какой закон должен прийти на смену гиперболическому? Смена закона может произойти либо вследствие катастрофы из-за слишком быстрого нарастания процесса, либо в результате плавного изменения характера роста. Рассмотрим последний, более благоприятный, случай.

Поскольку годовой прирост определяется разностью между рождаемостью и смертностью, его возрастание может происходить либо за счёт сокращения смертности, либо из-за увеличения рождаемости (либо по обеим причинам вместе). В последние столетия основную роль, по-видимому, играло сокращение смертности, вследствие успехов медицины, санитарно-эпидемических и других мероприятий. Сокращение смертности в целом, по всему земному шару, перекрывает уменьшение рождаемости в отдельных (особенно в развитых) странах, так что естественный прирост населения на Земле возрастает со временем. Менее ясно, почему он увеличивается столь же стремительно, как само население, что собственно и приводит к гиперболическому закону. Это пока остаётся загадкой. Тем не менее, можно считать, что в пределе, когда смертность достигнет минимальной величины (например, смертность от болезней и несчастных случаев в детском и производящем возрасте станет пренебрежимо мала), а рождаемость установится на некотором оптимальном уровне, определяемом совокупностью биологических, экономических и социокультурных факторов, — дальнейшее увеличение годового прироста прекратится, и население будет расти при постоянном годовом приросте, то есть экспоненциально.

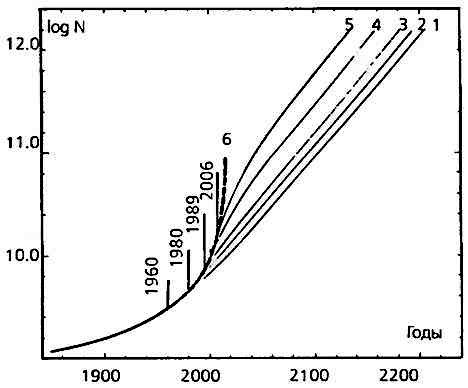
^{Рис.4. Переход от гиперболического закона на экспоненциальный (модель автора, 70-е годы XX века). По вертикальной оси — численность населения в логарифмическом масштабе. Кривые 1,2,3,4,5 — расчётные данные (экстраполяция) при различных значениях параметров модели, б — гиперболический закон роста}

Экспоненциальное развитие также приводит к бесконечной численности населения, но, в отличие от гиперболического роста, не на конечном, а на бесконечно длительном интервале времени. Практическое значение имеет вопрос о том, как скоро при экспоненциальном росте население Земли достигнет критической плотности. Последняя не обязательно зависит от истощения ресурсов, а может определяться социально-психологическими факторами. При переходе с гиперболического роста на экспоненциальный должна существовать промежуточная область. На рисунке 4 представлен рост народонаселения после перехода на экспоненту, согласно модели автора (70-е годы). Численные значения зависят от времени перехода и демографических параметров (фертильности и смертности), при которых стабилизируется относительный прирост населения. Для различных комбинаций параметров критическая плотность населения в 1 человек на 100 кв. метров суши для всего земного шара (а это плотность в современных крупных городах) достигается за время порядка нескольких сот лет.

Переход к экспоненциальному росту представляется наиболее естественным, ибо не требует никаких регулирующих воздействий. Однако это не единственный и, скорее всего, нереализуемый вариант. Существует ряд прогнозов численности населения Земли, в том числе, официальные прогнозы ООН [7]. Они дают достаточно разнообразный спектр возможностей, включая неограниченный рост и деградацию (уменьшение численности населения), начиная примерно с середины XXI века. Наибольший интерес представляет модель С.П.Капицы [6], которая приводит к стабилизации населения. Мы обсудим её в разделе 8 после рассмотрения результатов, к которым приводит учёт реинкарнаций. А сейчас подчеркнём: принципиальное отличие моделей с реинкарнацией состоит в том, что общая численность населения в обоих мирах — тонком и плотном — остаётся постоянной благодаря неизменному количеству монад.

Прежде чем перейти к обсуждению моделей с реинкарнацией, рассмотрим два вспомогательных примера.

4. Хождение по кругу

Пример 1. Пусть имеются два помещения, скажем, два зала (зал-1 и зал-2), заполненные людьми, которые постоянно переходят из одного зала в другой. Размеры залов для простоты примем одинаковыми. N₁ — число людей в зале-1, N₂ — число людей в зале-2, n₁₂ — число людей, переходящих из зала-1 в зал-2 в единицу времени, n₂₁, — число людей, переходящих из зала-2 в зал-1 в единицу времени. Условимся, что общее число людей N_o, равное сумме N₁ и N₂, остаётся неизменным.

Будем считать, что число переходящих пропорционально плотности населения в том зале, откуда переходят. Поскольку размеры залов приняты одинаковыми, это означает, что число переходящих пропорционально численности людей в соответствующем зале: n₁₂ = kN₁; n₂₁, = kN₂. Тогда изменение численности людей в каждом зале за малое время dt равно: dN₂ = (п₁₂ – n₂₁,)dt = k(N₁ – N₂)dt; dN₁ = (п₂₁ – n₁₂)dt = k(N₁ – N₂)dt = - dN₂. Решение уравнения для N₂ даёт: N₂(t)= [N_o-u_oexp(-2kt)]/2, где u_o = N_o-2N₂₀>0. При t → ∞ экспоненциальный член стремится к нулю, и N₂ (t) → N_o/2. То есть, каково бы ни было начальное распределение населения по помещениям, по прошествии достаточно большого интервала времени устанавливается равночисленное распределение: N₁ = N₂ = N_o/2.

Пример 2. Теперь несколько усложним задачу. Пусть помещения имеют разные размеры (разные площади). Для простоты положим, что они отличаются лишь длиной зала X, а ширина у обоих залов одинакова. Тогда плотность населения в каждом зале пропорциональна 1/Х. Если будем по-прежнему считать, что число переходящих из одного зала в другой пропорционально плотности населения в том зале, откуда переходят, то численность

N₂ = X₂{N_o - u_oexp[-kt(X₁ + Х₂)/Х₁Х₂] }/(Х₁ + X₂), где u_o = N₂₀ – N₂(X₁ + Х₂)/Х₂. При t → ∞ получаем: N₂ = N_oX₂/(X₁+X₂), N₁ = N_oX₁/(X₁+X₂), N₁/N₂ = Х₁/Х₂.

Итак, по истечении определённого времени процесс стабилизируется, и в обоих залах устанавливается постоянная численность населения, пропорциональная длине зала.

5. Квазистационарный процесс

Теперь перейдём к рассмотрению модели народонаселения с учётом реинкарнации. Рассмотрим два мира: мир тонкий (мир-1) и мир плотный (мир-2). Соответственно, все величины, относящиеся к миру-1, будем обозначать индексом 1, а все величины, относящиеся к миру-2, индексом 2.

N₁(t), N₂(t) — численность населения в соответствующих мирах в момент времени t; X₁, X₂ — средняя продолжительность жизни в них; n₁₂ определяет темп перехода из мира-1 в мир-2, это число жителей, переходящих из мира-1 в мир-2 в единицу времени; n₂₁ — число жителей, переходящих из мира-2 в мир-1 в единицу времени. Величина n₁₂, характеризует рождаемость в плотном мире, а величина n₂₁, — смертность.

Поскольку суммарно население в мирах не возникает и не уничтожается, а лишь переходит из одного мира в другой, в любой момент времени имеет место соотношение:

N₁(t) + N₂(t) = N_o = const.      (8)

Темп перехода зависит от численности населения в том мире, откуда происходит переход: n_ij = f(N_i), причём функция f(N_i) есть функция возрастающая, то есть число перешедших из мира-i в иной мир (число умерших в мире-i) при прочих равных условиях тем больше, чем больше население N_i этого мира. Предположим, что возрастающая функция f имеет самый простой вид: f(N_i) = k_iN_i; тогда n_ij = k_iN_i, то есть скорость перехода из данного мира прямо пропорциональна численности его населения. Коэффициент пропорциональности k_i представляет собой скорость перехода (число перешедших в единицу времени) в расчёте на одного жителя. Поэтому n₁₂.» = k₁N₁; n₂₁ = k₂N₂. Коэффициенты k₁, k₂ обратно пропорциональны соответствующим временам жизни: k₁ = k/Х₁, k₂ = k/Х₂.

Действительно, пусть среднее время жизни в мире-1 составляет 1000 лет, а в мире-2 — 100 лет. Тогда за время, пока один человек закончит свой цикл в мире-1 и перейдёт в мир-2, сто человек из мира-2 перейдут в мир-1. Итак: n₁₂ = kN₁/X₁; N₁₂ = kN₂/Х₂. Будем считать, что средние продолжительности жизни в обоих мирах неизменны: X₁ = const и Х₂ = const. Тогда выражения для числа переходов n₁₂ и n₂₁ полностью совпадают с соответствующими выражениями в рассмотренной выше задаче о переходе из зала в зал при различной длине залов, где вместо длин залов надо подставить значения средних продолжительностей жизни в мирах. Следовательно:

N₂ = X₂{N_o-u_oexp[-kt(X₁ + Х₂)/Х₁Х₂]}/(Х₁ + Х₂);      (9)

или при t → ∞ имеем:

N₂ = N_oX₂/(X₁+X₂); N₁ = N_oX₁/(X₁+X₂);

N₁/N₂ = Х₁/Х₂,

N₁₂ = kN₁/X₁ = kN_o/(X₁ + X₂),

N₂₁ = kN₂/X₂ = kN_o/(X₁+ X₂) = n₁₂.

Устанавливается стационарный процесс, когда прирост населения нулевой: ∆N = n₁₂ – n₂₁ = о. Сколько человек рождается в каждом из миров, столько же и умирает, численность населения в мирах остаётся постоянной.

Пусть в начальный момент времени справедливо: N₁₀ = N₀, N₂₀... = 0. Рождаемость в мире-2 в этот момент (точнее, в момент t_o + ε) максимальна (n_o = n₁₂ = kN_o/Х₁,), а смертность — нулевая (m_о = n₂₁ = N₂₀/X₂ = 0). С уменьшением N₁ рождаемость падает пропорционально N₁, а смертность растёт пропорционально возрастающему N₂ (m = n₂₁ = kN₂/X₂), пока не установится равновесие (n = m). Система приходит в стационарное состояние с постоянной численностью населения в мирах, пропорциональной продолжительности жизни в них (N₁/N₂ = Х₁/Х₂), Но это достигается лишь при бесконечно большом времени (t =∞). В любой другой сколь угодно большой момент времени распределение будет всё же отличаться от равновесного, асимптотически стремясь к нему, то есть будет протекать медленно затухающий процесс роста населения в мире-2 за счёт его сокращения в мире-1.

Как быстро устанавливается стационарный процесс? Практически процесс можно считать установившимся, когда вторым членом в фигурных скобках выражения (9) можно пренебречь. Обозначим: {u₀.exp [- kt(X₁ + Х₂)/Х₁Х₂] }/N₀ = α.

При α « 1 процесс можно считать установившимся. Для оценки надо знать зависимость α(t). При некоторых упрощающих предположениях, принимая, в частности, что Х₂/Х₁ = 0,1 и X₂ ≈ 100 лет, получим следующие оценки времени достижения определённого значения α :

Как видно, примерно по прошествии 700 лет вторым членом в выражении (9) вполне можно пренебречь (α = 0,001), то есть распределение станет достаточно близко к равновесному. 700 лет — это семикратная продолжительность жизни в мире-2, или 28 поколений, считая, что разница в поколениях составляет 25 лет.

Итак, процесс устанавливается довольно быстро. Но как долго он продолжается? Очевидно, до тех пор, пока выполняются условия постоянства длительности жизни: Х₁= const, X₂ = const. Можно думать, что они выполняются на протяжении большей части эволюционного цикла, но к концу цикла эти условия (или одно из них) нарушается, и процесс выходит из равновесия.

6. Когда люди спешат отдать долги: гиперболический рост

Как утверждается в эзотерической традиции, к концу цикла люди спешат перейти в мир-2 (плотный), чтобы завершить в нём свои дела, или заплатить кармические долги. Тогда продолжительность жизни в мире-1 (тонком) начинает убывать, сначала медленно, а затем, по мере приближения к концу цикла, всё быстрей и быстрей: X₁ ≠ const, X₁ =X₁(t).

Вместе с уменьшением продолжительности жизни в мире-1 рождаемость в мире-2 начинает возрастать, население его будет быстро увеличиваться, а население мира-1 — сокращаться. Что касается продолжительности жизни X₂, то хотя люди будут стремиться увеличить её, она не может выйти за естественные биологические пределы существования физического тела. Поэтому, если она и будет меняться, то гораздо медленнее, чем население N₂(t) в мире-2 (это и подтверждается статистическими данными), так что её, в первом приближении, можно считать постоянной: X₂ ≈ const.

Желающих (или потенциально готовых) перейти из мира-1 в мир-2 будет тем больше, чем больше численность населения N₁ и чем меньше продолжительность жизни X₁. Раньше мы считали, что все желающие перейти из мира-1 в мир-2 сразу реализуют это желание. Но теперь желающих становится столь много, что не все могут немедленно реализовать своё желание; ведь для того, чтобы воплотиться в плотном мире, каждый желающий должен найти для себя соответствующую супружескую пару, с помощью которой будет построено его физическое тело. Вероятность (Р) найти такую пару будет тем выше, чем больше численность населения N₂ в мире-2: Р = γN₂, n₁₂ = kγN₁N₂/X₁.

Будем считать, что смертность также зависит от времени, именно, n₂₁ = k₂N₂ = kγ(t)N₂/X₂, где γ(t) — убывающая функция, то есть с ходом времени смертность m = n₂₁ сокращается. В результате:

dN₂ = (n₁₂ – n₂₁)dt = N₂(t)[k γ N₁(t)/X₁(t) - k γ (t)/X₂]dt.      (10)

Выражение в квадратных скобках есть относительный годовой прирост населения q(t), 1-й член — относительная рождаемость, 2-й член — относительная смертность.

Вид функции q(t) существенно зависит от вида функции X₁(t). Каков он? С изменением продолжительности жизни X₁ меняется численность населения в обоих мирах. По мере сокращения X₁(t) численность населения N₁(t) тоже сокращается, по мере увеличения X₁(t) численность населения N₁(t) возрастает. Следовательно, с одной стороны, X₁ = F(N₁), где F — функция возрастающая. С другой стороны, X₁ как функция N₂ есть функция убывающая. Действительно, чем больше X₁, тем меньше рождаемость и тем меньше население ми ра-2. X₁ = f(N₂), где f — функция-убывающая. Примем зависимость X₁(t) в виде:

X₁(t) = a₁N₁(t)/[a₂N₂(t) + ψ(t)].      (11)

Если функция ψ(t), контролирующая рождаемость, связана с функцией φ(t), контролирующей смертность, соотношением ψ(t) = a₁φ(t)/γХ₂, то выражение в квадратных скобках уравнения (10) принимает вид: q(t) = N₂(t) kγa₂/a₁ = βN₂(t), где через β обозначена величина kγa₂/a₁. Тогда имеем: dN₂ = β[N₂(t)]²dt — что совпадает с выражением (5), которое соответствует гиперболическому закону роста народонаселения.

Функция ψ(t) также есть функция убывающая. При малых временах и рождаемость, и смертность велики, высокий прирост населения обеспечивается за счёт высокой рождаемости. С увеличением времени и смертность, и рождаемость падают, но смертность падает быстрее, перекрывая уменьшение рождаемости; теперь высокий прирост, обеспечивающий гиперболический рост народонаселения, достигается за счёт быстрого сокращения смертности даже при уменьшении рождаемости.

7. Стабилизация

Мы получили гиперболический закон роста народонаселения:

N₂(t) = 1/β(t_*-t),      (12)

Формально при t = t_* численность N₂(t) бесконечна. Это, конечно, невозможно, что отмечалось в разделе 3, но в нашей модели подобного и не должно быть, так как величина N₂(t) заведомо не может превышать суммарную численность N₀ = N₁₀ + N₂₀. При некотором значении t = τ_*, когда численность N₂ достигнет этой предельной величины, дальнейший её рост прекратится, всё население сосредоточится в мире-2, то есть цикл подойдёт к своему завершению. Теперь процесс должен устремиться в другую сторону: станет преобладать переход из мира-2 в мир-1. Будет ли он идти так, как описано выше — по квазистационарному сценарию, или ему будет предшествовать катастрофический переход в мир-1 — того мы не знаем.

Очевидно, что τ_* < t_*, так что момент времени τ_* должен наступить не позднее 2026 ÷ 2028 годов. Подставляя в выражение (12) численные значения параметров, найденные путём обработки статистических данных, получим: N₂(t) = 205,7 /(2028 - t), где t выражено в годах, отсчитываемых от начала новой эры, a N₂(t) — в миллиардах человек. При условии t = τ_*, численнocть N₂(t) = N₀= 205,7 /(2028 - τ_*).

Зная τ_*, можно определить N₀; зная N₀, можно найти τ_*. Но мы не знаем, чему равна исходная величина N₀, хотя возможно сделать ориентировочную оценку. Поскольку сейчас население Земли составляет порядка 6 млрд. человек, то очевидно, что численность N₀ больше 6 млрд. А так как процесс уже вышел из стационарного состояния, когда имело место соотношение N₁/N₂ = Х₁/Х₂, то сейчас численность N₁ заведомо меньше 60 млрд., а N₀ меньше 66 млрд.; в результате, имеем пределы для численности в млрд.: 6 < N₀ < 66.

Задаваясь различными значениями суммарной численности N₀, получим следующие значения для предельной величины τ_*, когда условно всё население сосредотачивается в плотном мире:

При N₀ = 60 млрд. чел. величина τ_* практически не отличается от t_*.

Конечно, маловероятно, чтобы гиперболический рост шёл вплоть до полного опустошения миpa-1 (N₁ = 0, N₂ = N₀) — подобно песочным часам, в которых весь песок пересыпается из верхней колбы в нижнюю, после чего процесс останавливается, и чтобы запустить его вновь, часы надо перевернуть. Скорее всего, переход к стабилизации (если не произойдёт катастрофы) будет постепенным. Можно на качественном уровне, без построения количественной теории, указать некоторые причины стабилизации. 1). После того, как значительная часть населения мира-1 перейдёт в мир-2, «очередь» на входе в мир-2 «рассосётся». Теперь все желающие вновь получат возможность воплощения, и необходимость введения вероятности Р = γN₂ в формулу (10) отпадает. Поэтому квадратичная зависимость от N₂ уже не может иметь места, 2). Когда «долги» в основном будут исчерпаны и в мире-1 останутся лишь те, кто недавно перешёл туда, рассчитавшись по долгам, необходимость в сокращении длительности жизни X₁ в мире-1 также отпадёт; длительность X₁ вновь становится постоянной. Отказ от введения вероятности Р = γN₂ приводит к переходу на экспоненциальный рост, а отказ от условия X₁ = X₁(t) возвращает нас вновь к квазистационарному процессу, но уже при новых начальных условиях, сложившихся к тому времени.

8. Обсуждение модели

Итак, учёт реинкарнаций приводит к следующей картине изменения численности населения Земли: в эпоху, далеко отстоящую от современного момента, население Земли изменялось очень медленно, практически оставаясь постоянным; затем произошёл переход к гиперболическому росту, при котором по мере приближения к характеристическому моменту времени t_* численность населения стала нарастать лавинообразно («демографический взрыв»); и, наконец, третий период, который, по всей видимости, соответствует современному моменту, отличается переходом к постоянной численности населения (стабилизация). Качественно эта картина совпадает с наиболее развитой современной моделью роста народонаселения Земли, предложенной С.П.Капицей [6]. В ней, по-видимому, впервые удалось описать закономерности роста народонаселения Земли на огромном промежутке времени от «происхождения человека» до наших дней. Длительность этого периода, по данным современной антропологии, около 4,5 миллионов лет. Капица разделяет его на три эпохи: раннюю эпоху А, когда население росло очень медленно, изменяясь от нуля пропорционально величине -ctg t; основную эпоху В, когда наблюдается гиперболический закон роста и относительная скорость q = 1 /N(dN/dt) непрерывно увеличивается; позднюю эпоху С, для которой начинает сказываться ограничение на относительную скорость q ≤/τ (τ — параметр модели, имеющий размерность времени). В эту эпоху население растёт пропорционально arcctg [(t_* - t)/ τ ]. При условии t →∞, (t_* - t) → - ∞, численность N → К²π (К — безразмерный параметр). Предельное значение N для различных параметров модели получается от 10 до 25 млрд. чел. Капица показал, что изменение численности населения во все три эпохи может быть описано общей формулой, и определил временные границы перехода от одной эпохи к другой. Эпоха А началась около 4,4 млн. лет тому назад и длилась 2,8 млн. лет; около 1,6 млн. лет тому назад она сменилась эпохой В, длящейся почти до современного момента и охватывающей палеолит, неолит и весь известный исторический период развития человечества². Переход к эпохе С приходится на последние десятилетия XX века.

Что касается гиперболического закона роста, то он является частным проявлением более общей зависимости: N = С (t₁ - t)^k, из которой при k = -1 следует гиперболический закон. Капица обращает внимание на то, что такая зависимость применима к довольно широкому классу явлений (изучаемых синергетикой. — Ред.), ведущих к так называемому режиму с обострением. Таким образом, описываемый гиперболическим законом «демографический взрыв» представляется как «глобальная системная неустойчивость», характерная для процессов роста в существенно нелинейных системах. Это позволяет определить место демографических процессов в ряду математически подобных систем, однако, не даёт конкретного объяснения, конкретного механизма реализации гиперболического роста. Квадратическую зависимость от N в выражении (5), согласно Капице, можно рассматривать с системной точки зрения как результат коллективного взаимодействия — не только биологического (которое является бинарным по своей природе), но и социального и экономического, поскольку все эти факторы регулируют рост народонаселения. То есть, это результат некоего единого статистического процесса, механизм которого модель не раскрывает. В предлагаемой же модели с реинкарнацией делается попытка вскрыть возможный механизм, приводящий к гиперболическому росту (выделено ред.). Разумеется, как и во всякой модели, приходится делать определённые предположения, которые в рамках модели представляются разумными.

Весьма важным для модели Капицы является наличие единой демографической системы для всего населения Земли. Но обоснование этого положения сталкивается с определёнными трудностями, ибо несмотря на наличие торговли, удалённые регионы в прежние эпохи были очень слабо связаны между собой. Как отмечает сам Капица, процесс объединения мира в единую демографическую систему начался уже после Великих географических открытий и завершается как раз в наше время [6], с. 70. Но для того, чтобы модель «работала», единая демографическая система должна была сложиться ещё в эпоху А, то есть миллионы лет назад! В предлагаемой модели с реинкарнацией этой трудности не возникает: всё население мира с самого начала представляет собой единую систему, так как люди (точнее, монады. — Ред.), жившие в одних регионах, в последующих инкарнациях воплощаются в других (выделено ред.).

Заключение

Настоящая работа представляет собой попытку рассмотреть закон роста народонаселения (построить математическую модель) с учётом идеи реинкарнации. В этом смысле, она имеет скорее методологическое значение. Показано, что можно удовлетворительно описать основные закономерности роста. Отметим следующие основные результаты.

1. Вывод об установлении квазистационарного процесса регулирования населённости в двух мирах, именно — пропорциональной продолжительности жизни в них, независимо от начальных условий, но при соблюдении условия постоянства времени пребывания в каждом из миров (X₁ = const, X₂ = const).

2. Переход от квазистационарного процесса к гиперболическому закону роста народонаселения в конце цикла, когда это условие нарушается.

3. После прекращения стационарной фазы первое время высокий годовой прирост, обеспечивающий гиперболический рост народонаселения, достигается за счёт высокой рождаемости при довольно большой смертности. С течением времени и рождаемость, и смертность сокращаются, но смертность падает быстрее, перекрывая уменьшение рождаемости. И высокий годовой прирост достигается из-за быстрого сокращения смертности даже при уменьшении рождаемости.

4. Модель не приводит к бесконечной численности населения в силу условия сохранения общей численности (N₁ + N₂ = N₀)³. По мере сокращения населения в мире-1 условия для гиперболического роста в мире-2 исчезают, и процесс стабилизируется.

5. Качественно модель с реинкарнацией описывает те же фазы роста населения, что и модель Капицы [6], но для неё пока не получено универсальной формулы, справедливой для всех трёх фаз, и не найдены аналитические выражения для перехода от одной фазы к другой. К достоинствам предлагаемой модели можно отнести то, что она позволяет раскрыть «демографический механизм», действующий в каждой фазе, в том числе, механизм того коллективного статистического процесса, который, согласно С.П.Капице, приводит к гиперболическому росту.